元生技データサイエンティストのメモ帳

勉強したことの備忘録とか雑記とか

はじめての自作キーボード作成記（Keyball61）

1ヶ月ほど前に自作キーボードの 沼 世界に足を踏み入れ、苦労しながらも先日Keyball6を完成させることができました！

今回は作成に合わせて揃えたものや完成までに苦労した点をまとめます。

Keyball61を買おうと思ったきっかけ

今までHHKB BTを使っていてそこそこ満足していたのですが、

  • 分割されてないキーボードだと仕事中に取れる姿勢が限られるので、姿勢を楽にする目的で分割キーボードに興味が出てきてた
  • キーボードを新調するなら、トラックボールがセットになってるものが欲しかった

というわけでこの条件に合うキーボードを探したところ、Keyball61と出会いました。

Keyball61は自分で組み立てが必要な自作キーボードなわけですが、関西Kaggler会などの場で自作キーボードの話を聞いていて心理的なハードルが下がっていたことからチャレンジしてみることにしました。

準備編

兎にも角にも必要なものを揃えないと始まりません。
初めての自作キーボード作成だったこともあり、色々買いました。

キーボード本体

「Keyball61を作るぞ！」と決めた時は白銀ラボでも遊舎工房でも売り切れだったので、入荷通知のメールを登録してしばらく待ちました。
数週間かかるのも覚悟しましたが1週間ほどで入荷メールをいただいたので速攻で確保しました。

このブログの執筆時点ではそこそこ在庫があるようです。

shirogane-lab.net

【委託】Keyball61shop.yushakobo.jp

ビルドガイドのもある通りこのキットだけではキーボードは完成しないので、以下のもの用意しました。

道具類

元々家にあったこちらのハンダごてにC型のこて先をつけて作業しました。
20Wほどのものなので昇温に時間がかりますが、LEDのハンダ付け以外は十分こなせます。
後述の温度調整できるものよりもこて先が大きいので部品に熱が伝えやすいのが良き。

goot(グット) 一般電気用はんだごて ニクロムヒーター KS-20R 日本製

goot(グット) 一般電気用はんだごて ニクロムヒーター KS-20R 日本製

  • 太洋電機産業(goot)
Amazon
goot(グット) 替こて先 径4×75mm R-48C 日本製

goot(グット) 替こて先 径4×75mm R-48C 日本製

  • 太洋電機産業(goot)
Amazon

ハンダはこちらの鉛フリーのφ0.8mmのものを使用しました。

akizukidenshi.com

基本は上記のものでハンダ付けを進めていたのですが、ハンダ初心者が熱に弱いLEDを「温度調整できないハンダごて」で「鉛フリーのハンダ」でやるのは無理があったようでLEDをいくつか壊したため、温度調整できるハンダごてを追加で購入しました。
私が買ったものは以下のもので、USB Type-Cで給電できて取り回しが良く、65Wなので昇温が早いので使いやすかったです。
温度調整して以降はLEDが壊れることはほぼなくなったので、LEDのハンダづには温度調整できるハンダごては必須ですね。

https://a.aliexpress.com/_om2ev9a

あとはハンダに必要はハンダごての台やフラックス、フラックス洗浄剤を買ってます。

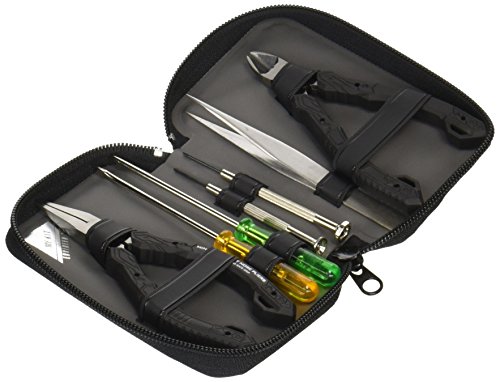
あとはピンセットや精密ドライバーがなかったのでこちらを購入しました。
必要なものが収納に便利なポーチに入っているので、何かと便利です。

ENGINEER エンジニア マイキット 7点セット KS-01

ENGINEER エンジニア マイキット 7点セット KS-01

  • ENGINEER
Amazon

完成までの道のり

ハンダ付け自体が初めてだったので、結構時間がかかりました。
ハンダ付けし始めたの12/23、完成したのが1/21と1ヶ月ほどかかっています。

（まぁその間に統計検定準1級を受けたり年末年始を挟んでいるので、ずっと作業をしてたわけでもないですが）

慣れていない作業ということもあって色々失敗もしたので、これから作るひとの参考になるよう自分の失敗をつらつら書いていこうと思います。

失敗談1 Key Microのハンダ付け失敗

Key Microをハンダ付けする際に加減がわからず、スルーホールに刺したピンの周りにハンダが貯まらないのでドンドンハンダを足していったのですが、気づくとピンソケットの中にハンダが詰まりまくっていて大変なことになりました。
しかもKey Microの裏表を間違えるという有様。ビルドガイドはちゃんと読もう！

ハンダ吸い取り機を買ったりしてピンソケット取り外しを試みるもなかなかうまくいかず、最終的にはピンソケットをペンチで破壊してKey Microを救出しました。

お高いKey Micro救出のために結構な時間がかかったので「お高い基板じゃなければ諦めて基板ごと書い直す決心がつくのに。。」と思いながら作業したのはいい思い出ですw

失敗談2 ハンダ付けしたLEDが光らない問題

LEDが光らない原因は自分の場合は2パターンあって、「ハンダごての熱でLED自体が壊れてる」か「LEDに異常はないがハンダ付けをミスってる」でした。
どちらかというと後者が多い印象でした。

後者を疑ってハンダ吸い取り線で余分なハンダを吸い取ると復活することが多かったです。
（見た目ではわからなかったが、隣合ったパッドのハンダが繋がってたか？）

それでもダメな時は前者を疑って新しいLEDにすると、だいたい治りました。
LED自体が壊れるのは、温度調整できるハンダごてにしてからはほぼなくなったので、最初から導入しておけばとは思いました。

ちなみに「光らないLED」ができてしまった時の対処としては、こちらのサイトで紹介されている「点灯していない LED の一つ前にある点灯している LED の DIN と、点灯していない LED の DIN をジャンパワイヤーなどで接続する」と良いというのが非常に役立ちました。
この結果から「どこが大丈夫でどこがダメか」の切り分けができるので、トラブルシュートに役立ちます。

kankodori-blog.com

それにしてもTRSケーブルで繋いだら光らなくなったり、突然たまに「玉切れした蛍光灯」みたいな光り方するのはホンマに謎。電気全然わからん。

失敗談3 基盤のパターン破壊

熱で壊してしまったLEDを外す際に銅箔ごと剥がしてしまい、その場所にハンダ付けしても電気が流れないという事態に陥ってしまいました。

色々調べた結果「壊したパターンの場所をジャンパー線で繋ぐ」しかないようだったので、↓のように短く切ったジャンパー線をハンダ付けして事なきを得ました。

見た目がかなりイマイチですが、組み立てて仕舞えば見えない場所なので気にしない方向で。

失敗談4 買った部品の規格が合わない問題

これは色々やらかしました。

端子が太いTRSケーブルを買ってしまったり、

データ通信非対応のUSBケーブルを買ってしまったり、

用意したキースイッチに対応していないキーキャップを買ってしまったり、

MBK Choc Low-Profile Keycapsshop.yushakobo.jp

などなど、無駄な買い物を結構してしまいました。

失敗談5 OLEDにハンダごてが接触

こちらの写真をご覧ください。

OLEDのハンダ付けの際に本体にハンダごてが当たってしまい、OLEDの右下が少し変色しています。
やらかした時はテンションが下がりましたが動作はするのでそのままにしています。
ピンホールのハンダ付けの際のハンダごての向きには注意しないといけなかったですね。

作ってみての感想

そんなこんなで色々苦労しましたが、なんとか完成しました。

使ってみての感想としては、 - 姿勢が楽 - 1箇所で全ての操作が完結するのが最高 - キーマップを色々変更できるので、カスタマイズの幅が広い

特に姿勢は↓の写真のように椅子の肘置きの目の前にキーボードを置いて、肘置きに手首を乗せて操作するスタイルがかなり快適です。
もう猫背にならずに済みます。

ただキーボードの配列が変わった関係で、タイピング速度は落ちました（今は下よりマシです）。

まぁ慣れの問題なので時間が解決してくれるでしょうし、この記事を書いている間にタイピング速度はマシになってきたように感じます。

あとはまだできてないですが、ファームを自分で書き換えてマウスカーソルの速度やスクロールの設定値だったりをカスタマイズするともっと便利になりそうです。
まだまだ未開の地があるので、これからも色々試してみるのが楽しみです。

.

そんなこんなではじめての自作キーボード作成記でした。
ここまでお読みいただきありがとうございます。

統計検定準1級の勉強に役だった書籍まとめ

データ分析 データサイエンティスト

統計検定準1級にに3回目の挑戦で合格できました。

今回は試験を受けるまでに参考にした書籍をまとめます。

公式テキスト類

これは外せないですね。まずこれをやって、全体感を掴みましょう。
ワークブックの方は膨大な範囲を1冊に収めている関係で、1回読んだだけで理解するのはなかなか骨が折れると思います。
私は途中でKaggleのコンペに出たり、スクラムマスターの資格を取ったりと色々他にも手を出しながらだったので、読み終わるのに1年近くかかりました。

ワークブックの内容をある程度理解したら後述の過去問に移って、わからないところが出てきたらこちらのテキストに戻る、ぐらいの進め方が良さそうです。

日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック

日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック

  • 学術図書出版社
Amazon

日本統計学会公式認定 統計検定 準1級 公式問題集

日本統計学会公式認定 統計検定 準1級 公式問題集

  • 実務教育出版
Amazon

副読本

基本は上記の流れなんですが、この2冊だけでは理解が難しい部分があります。
ここではそういう部分の理解の助けになった書籍を紹介します。

PRML

2章で共役事前分布や逐次推定の話を、3章からは線形モデルの話を徹底的にやってくれます。
演習の計算は大変ですが、根気よくやり切れば間違いなく実力がつく1冊です。

パターン認識と機械学習 上

パターン認識と機械学習 上

Amazon

アイシアさんの動画

学生時代から線形代数が大の苦手な私ですが、「固有値固有ベクトルがわかると何が嬉しいか」というようなことを順を追ってわかりやすく説明してくれるので、動画のキャッチフレーズの通り「行列の積と和解」を果たすことができました。
線形代数に苦手意識のある方におすすめです。

2級→準1級の大きな違いの1つが「多次元のデータを扱うために行列演算を頻繁に使う」なので、線形代数に慣れ親しんでおくことはかなり重要だと思っています。

youtube.com

入門 機械学習による異常検知

「異常検知」に特化した本書には、統計検定準1級の知識多く用いられます。
基本的な統計解析から始まり、本書の後半では主成分分析や線形回帰モデル、自己回帰モデルなどによる異常検知が丁寧に解説されています。
試験に直接役立てられるわけではないですが、試験勉強を通して得た知識にこういう使い方もあるのかと気づかせてくれる1冊です。
試験に受かってからもう一度ちゃんと読み直したい1冊でもあります。

入門 機械学習による異常検知―Rによる実践ガイド

入門 機械学習による異常検知―Rによる実践ガイド

Amazon

あつまれ統計の森

過去問で行き詰まった際、こちらのサイトの解説にかなりお世話になりました。

www.hello-statisticians.com

私が読んだ本で準1級の範囲に関わっているものはこんなところかなと。
振り返ってみるとワークブック以外で「統計検定のためだけに買った」という本が思いのほか少なかったですね。

もっと試験範囲全体を見渡して様々な書籍を紹介してくれているサイトがあるので、そちらの方が役立つかもしれませんw

試験に受かったものの因果分析あたりは理解が浅いのでもっと勉強したいところです。
良書をご存知の方、教えていただけるとありがたいです。

お読みいただきありがとうございました。

関西Kaggler会 参加レポ

先日参加した関西Kaggler会が楽しかった + 勉強になったので、忘れないうちにまとめておこうと思います。

オープニング

まずはいつもの「始まりの儀式」で開始。
過去の写真と見比べるとすごく参加者が増えましたね！

そしてmgnさんのオープニング。
いい感じに会場を暖めて笑いも引き出すトークは流石です。

「どんどんツートしましょう」ということでこんな仕掛けが。
他のイベントでも使えそうです。

ちなみに関西は「お行儀いい関東と違って笑いも」とのことです。

これは突然イジられるベルーガさん。

どりぃさん発表

まずは会場を提供くださったR3 instituteからどりぃさんが登壇。
素敵な会場を使わせていただき、ありがとうございます。
以下のリンクに会場の詳しい説明や写真があります。

たいちさん発表

ここからKaggleの話、と思いきや自作キーボードの話。

ちなみにこのレポの筆者はHHKBを愛用しています。
HHKBと同じぐらいの出費で自作キーボードの世界に入門できるそうで、かなり興味が湧きました（特に左右分離してるやつ）。

あと「自作キーボードを使うと持ち歩かないといけなくて重いんですが、、」という質問に「なら2つ持てばいい」と食い気味に回答していて、ここでも爆笑がw

ちなみに「持ち運ぶことが気にならなくなるくらい楽しい」とのことです。

ころんびあさん発表

続いてのころんびあさんの発表は「コンペに勝つには」。
こちらはコンペはコンペでもCVPRのお話。

ただ入りが全員で爆笑していただけに、技術の深い話になるとなんか会場が異様に静かに。。
（全員が全員画像のプロじゃないだけに、この辺の塩梅はすごい難しいですね）

結果、結論としては「いい感じに」やるということに。
（以降「いい感じに」「よしなに」が会場で流行り出すw）

ちなみに3D物体検出を「いい感じに」やれるようにはなるには、「とにかく論文読みましょう！」とのこと。
（後どれぐらい論文を読めば「いい感じに」扱えるようになるだろうか）

T88さん発表

こちらは関西Kaggler会に先立って開催されたコミュニティコンペをGPT-4にコードを書かせてみた、というもの。

こちらは「githubのissueにcv改善のアイディアを書けば、GPT-4がコードを書いてくれてcv下がったか確認してくれる」という優れもの。

ちゃんと確認しないと初歩的なミスをしたり、存在しない列名を指定してエラーを出したり、盛大にリークさせたりするものの、最終的にはなんとコミュニティコンペで11位相当スコアだったとのこと。

（このブログの筆者はギリギリでした。ただ私のsubmitは「特定の市の不動産価格を1.3倍する後処理」を入れているので、それを入れない条件で揃えるとGPT-4に負けます）

ronさん発表

お次はパパさんKagglerで社会人博士で出張の多いronさんによる「時間のないKagglerのすすめ」。

「いかに隙間時間でKaggleをするか」がポイントとのこと。

スマホからGPUマシンにアクセスしたり、
子どもを寝かしつけながらスマホでdiscussion読んだり、
スマホでsubmitしたり、

とにかくスマホを大活用してます（キーボードいらないとか言わない）。

関東Kaggler会でも「Redbullは1日1本まで」と言うお話でしたが、こちらでは「RedbullとChilloutを交互に飲む」メソッドが紹介されてました。
（ronさん、お身体は大事にしてください。。）

あと「大自然の中でsubmitするといいスコアが出る」と言うお話でしたが、、

Jackさん発表

お次はJackさんから「Feature Importanceによる特徴量選択とリーク」のお話。

speakerdeck.com

Jackさんは少ないsub数で上位に入ることから「忍者」と呼ばれているそうで。

CV全体でFeature Importanceを平均しちゃうと、バリデーションデータのノイズ情報も入り込んでしまうとのこと。
あとは「全foldで改善しているか」と言う観点も重要だそうで。
その辺りを真面目に見ないことがあるので気をつけたいところです。

くるぴーさん発表

お次は最近Grand Masterに昇格されたくるぴーさんのLLMコンペの話。

実験を高速に回すコツを色々伺えました。

また「❌GPUを止めるな ⭕️思考を止めるな」「信じたアイディアと心中する」など、私含め多くのKagglerに刺ささる名言をいただきました。
（疲れてくると適当にハイパラだけ変えてGPU動かしたりしがち。。）

nejumiさん発表

お次はこの関西Kaggler会に先立って行われたコミュニティコンペを設計くださったnejumiさんから、まさしくコミュニティコンペの話。

speakerdeck.com

ここ数年で、商用利用がOKになったり、Visibilityが制御できるようになったり、Custom Metricが使えるようになったりと、何かと機能が増えて便利になっているようです。
「コンペ設計のポイント」という「開く側」でないとノウハウを積めない貴重なお話も伺えました。
「コンペを開く側」お話はなかなか伺えないので、非常に興味深かったです。

職場の有志とかでコミュニティコンペを開くのも面白そう、と思えるお話でした。

あとチーターは丸わかりらしいですよ！

johannyjm1さん発表

お次はjohannyjm1さんの「Polarsと遅延評価」

筆者は「遅延評価」をちゃんと分かってなかったのですが、"式の評価を「必要になるまで」行わない、サボる仕組みのこと" とのことです。
気になる方は↑の資料が非常にわかりやすいのでそちらをご覧ください。

polarsを使う時は、"df.lazy()" で遅延評価を使いましょう！

あまえびんさんLT

お次はあまえびんさんの「オレオレ開発Kaggle環境」。

speakerdeck.com

筆者はKaggle用のAWS環境を立てる際、これまではAWS推奨のTraning job用のDoeck imageを使ってましたが、ライブラリのバージョンやディレクトリの構成も考えるとKaggleに合わせたイメージを使う方が良さそうです。
今度からそれで開発してみようと思います。

すでに「オレオレ開発Kaggle環境」のユーザーもいらっしゃるようです。

ベルーガさんLT

お次はベルーガさんのLT。
ここはその場限りの話が多かったため、割愛させていただきます。

paoさんLT

最後はpaoさんのLT。
ABEJAさんの紹介や、Kaggleと実務に関して「Kagglerのどんなところが実務の中で役立っているのか」「Kagglerの安心感」などの話でした。

懇親会

夜の懇親会では新しくGMに上られたchunmajinさんとくるぴーさんに運営からお祝いにTシャツのプレゼントがあったり、

抽選会があったり、

コンペの賞の贈呈があったり

とイベントが盛り沢山な上に、普段そうそう会えない方々とお話しすることができ、大盛り上がりの楽しい & 勉強に場でした。

以上、関西Kaggler会 参加レポでした！
少しでも雰囲気をお届けできていたら幸いです。

最後に、このような非常に勉強になりかつ楽しい場を設けていただいた運営の方々、末筆ながら感謝申し上げます。
会場でお話しいただいた方々も、本当にありがとうございました！

なぜ近年AIが活用されるようになったかを考える

近年「AI」という言葉を耳にする機会が増えてきたかと思います。
今回は近年AIがここまで活用されるようになった要因を、デープラーニングがどのように画像分類を行なっているかを紐解いていきます。

AIの歴史

「Artificial Inteligence(AI, 人工知能)」という言葉が初めて登場したのは1956年に開かれた「ダートマス会議」で、そこでAIに関する研究が学術研究の1分野として確立したと言 われています。そこから第一次AIブーム（1950年代後半〜1960年代）、第二次AIブーム(1980年代)を経て、2000年台から第三次AIブームが始まり、現在も続いています1)。
まずは第一次〜第三次AIブームそれぞれを振り返ってみたいと思います。

第一次AIブーム

1956年に開かれた「ダートマス会議」で Artificial Inteligence（人工知能）という言葉が初めて登場し、AIに関する研究が学術研究の1分野として確立しました。
探索木など、「推論」や「探索」の研究が進んで特定の問題を解くことができるようになったことから、注目を集めました。
ただし研究が進んで当時の技術では迷路やパズルのような限定された問題（トイプロブレム）しか解けず、現実世界に存在する複雑な問題が解けないことがわかると、ブームが収束しました。

第二次AIブーム

第二次AIブームは1980年台に始まりました。
知識をいかに表現するかという研究が盛んに進められ、専門家の「知識」をコンピュータに与えることで「エキスパートシステム」が開発できるとして研究が進められました。
知識はIF-THENルールで記述されることが想定され、このルールを大量に貯めておけば最高の専門家の思考過程を再現できると考えられていました。 この試みは研究が進むにつれて以下の問題が明らかになり、期待が失望に変わり、ブームは収束しました。

  • 「常識」など広い範囲の知識を蓄積・管理するのに膨大な労力を要すること
  • 人間が明確に列挙できるルールの多様性が、現実世界の多様性に比べて桁違いに乏しいこと

第三次AIブーム

第三次AIブームは2012年ごろから始まりました。
きっかけは深層学習（ディープラーニング）を活用したAlexNetというアルゴリズムがILSVRC (ImageNet Large Scale Visual Recognition Challenge) という画像に写っているものを分類するアルゴリズムの精度を競うコンペティションで、これまでのtop5エラー率※を大幅に更新したことです。
※アルゴリズムが各写真に写っているものとして予想した上位5つに正解が含まれていない割合

これはインターネットの普及に伴うビッグデータの拡大やコンピュータの演算処理能力の向上によるところも大きいですが、ディープラーニングが「特徴量」と「関数」を自ら習得できるようになったことが大きいです。

次の章ではこの「特徴量」と「関数」に関して説明していきます。

特徴量と関数について

特徴量とは

特徴量とは分析対象データの中の、予測の手掛かりとなる変数のことです。
簡単な例で説明していきたいと思います。

例として以下の様な「気温とアイスの売り上げ個数」のデータ（架空のデータ）がある場合を想像してください。

気温とアイスの売り上げ

データから「気温が上がるとアイスの売り上げ個数が増える」というのが想像できるかと思います。また「気温が高い方がアイスを食べたくなる」という直感に反していないので、前述の「気温が上がるとアイスの売り上げ個数が増える」は理解しやすいかと思います。

気温はアイスの売り上げ個数の予測の手がかりとなるので、気温はアイスの売り上げ個数の特徴量と言えます。

関数とは

先ほどの例で特徴量からアイスの売り上げを予測するには、グラフ上の点のできるだけ近くを通る直線（図の赤線）を引けば可能となります（この直線を引くには最小二乗法などの手法がありますが、ここでは割愛します）。

このように特徴量（気温）から求めたい変数（アイスの売り上げ）を予測する式を「関数」といいます。

ディープラーニングはどのように特徴量と関数を扱っているのか

まずは特徴量をディープラーニングでどのように扱っているかを見ていきたいと思います。
気温とアイスの例で特徴量を考えるのは簡単でした。それはデータがすでに「売り上げ個数」と「気温」という数値データになっているからです。

これに対して「画像に何が写っているか」を判定する場合の特徴量を考えてみましょう。

例えば「画像にリンゴが写っているか」を考えると「赤いか」「丸いか」など言葉として羅列することはできますが、それをコンピュータでも処理できる形で数値化するのは非常に難しいと感じるかと思います。
また例え数値化できたとしてもリンゴ以外のあらゆるものに対応しようとすると、ルールが膨大になるのは想像に難くありません。

この問題に対してディープラーニングではどのように対応しているのでしょうか？
「第三次AIブーム」の節で紹介したAlexNetの1層目の畳み込み層パラメータを図示すると、下図のようになっています2)。
上3列の48個の畳み込み層で境界線に関する特徴を、下3列の48個の畳み込み層で色に関する特徴を抽出していると言われています。

AlexNetで抽出した画像の特徴量

AlexNetでは「畳み込み層」と言われるニューラルネットワークに画像を学習させることで上記のような特徴量を抽出できるようになりました。人が特徴量の抽出方法を1つ1つ教えるようなことはしていません。

このように人が理解できる形では数値化されていないデータ（非構造化データ）から特徴量を抽出する仕組みができたことが大きなブレイクスルーだったと言えます。

「畳み込み層」の仕組みに関しては以下の動画がわかりやすいので、そちらをご参照いただければと思います。

www.youtube.com

次に関数についてです。
ディープラーニングでは前述の畳み込み層などで抽出した特徴量を「全結合層」と呼ばれるニューラルネットワークで処理しています。
全結合層では全ての変数を使った一次関数と非線形な活性化関数を組み合わせた単純な機構（場合によっては全結合層を複数回繰り返して）で、複雑な関数を表現できるようになっています。
これによって特徴量を欲しい出力（画像に何が写っているか、など）

全結合層の仕組みに関してはすでにわかりやすく解説したサイトがたくさんあるので、詳細の説明はそちらを参照いただければと思います。
例えば以下の動画が参考になると思います。

www.youtube.com

このようにディープラーニングでは、画像のような人が理解できる形では数値化されていない非構造化データから特徴量を抽出する方法をデータから学習し、全結合層でその特徴量に対する関数を作って目的とする出力に変換する複雑な関数をシンプルな機構で実現しました。
これこそがデープラーニングがここまで色々なものに適用されるほど高い性能を出せた要因であったのではないかと考えています。

まとめ

本日はデープラーニングがどのように画像分類を行なっているかを紐解くことで、「なぜ近年AIが活用されるようになったか」を考えてみました。
最近流行っている「お絵描きAI」のようなツールはここからさらに技術的な進歩があったので、また別の機会にまとめてみようと思います。

お読みいただき、ありがとうございました。

1) https://www.soumu.go.jp/johotsusintokei/whitepaper/ja/h28/html/nc142120.html
2) https://proceedings.neurips.cc/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf

技術同人誌出版によせて

9月10日から開催の技術書典13で技術同人誌を出します。 今回はその本に関してを書いていきたいと思います。

techbookfest.org

本の内容

まずは「なぜAI活用に取り組むのか」を説明したあと、Azureとそこで提供されているサービスCognitive Servicesについてを説明し、Cognitive Servicesの「視覚」に関する機能の使い方を紹介しています。

目次は以下の通りです。

  1. ノンプログラマーがなぜ今「AI活用」に取り組むべきなのか
  2. Azureとは
  3. 必ず抑えておきたいセキュリティとコストの話
  4. Azure Cognitive Services について
  5. Azure Cognitive Servicesを使ってみる
  6. おわりに

なぜCognitive Servicesを紹介するのか

いわゆる「第三次AIブーム」以降、主に深層学習を活用した機械学習モデルの性能向上を背景にAI技術活用が進んできました。第三次AIブーム当初は専門家がコーティングしないと活用できませんでしたが2017年に「AIの民主化」が提唱されて以降、ノーコード、ローコードでAI技術を活用できるようなサービスが出てきました。そのようなサービスの1つであるAzure Cognitive Servicesを通じて「今までAIが身近でなかった人にも、自分でAIを触れるようになれば」という思いがあり、本にまとめることにしました。

「第三次AIブーム」が始まってから10年近く経過しAIの活用が進んでいますが、AIが活用されている範囲は限られていると思います。そのような状況を変えていく手段の1つとして、「ITやAIには疎くても、自分がいる業界のことには詳しい人」に「AIが何をできるか」を知ってもらい、その人が詳しい分野にどうAIを活用すると役立つかを想像してもらうのが重要ではないかと考えています。それによって「AIや機械学習に関しては詳しいが、業界に関しては知らない人」だけでは思いもよらないような、面白いAI活用方法が産まれてくるのではないかと思っています。

今回私が書いた本を通じて「AIでこんなことができるんだ」と気づいて、AI活用に興味を持ってくれる方が一人でもいらっしゃれば幸いです。

techbookfest.org

ギリギリ銅メダルを取れたKaggle Feedback Prizeを振り返る

こんにちは。sue124です。

まだ順位は確定してませんがPublic Scoreでギリギリ銅メダル圏内に入れたので、やったことを振り返ってみたいと思います。

Kaggle Feedback Prizeとは

Feedback Prizeのタスクは自然言語処理（NLP）の中でも固有表現抽出（NER）と呼ばれるものです。

具体的にいうと、学生が書いたレポートの中から以下に該当する部分を抽出できる機械学習モデルを作るタスクです。

  • Lead (赤)
  • Position (緑)
  • Evidence (黄)
  • Claim (青)
  • Concluding Statement (マゼンタ)
  • Counterclaim (シアン)
  • Rebuttal (灰)
  • None (無色)

学習データとして与えられている文章にわかりやすく色づけすると、以下のようになります。

f:id:sue124:20220317171112p:plain

学習データから作成した機械学習モデルでテストデータの文章のどこが何に該当するかを予測し、正解と比較した際のmacro F1 scoreで順位が決まります。

評価方法の詳細は以下のリンク先の通りです。

www.kaggle.com

コンペ内でやってみたこと

今回コンペの中でやったことは以下の通りです。

  • Base Lineモデルの改造
  • Threshold微調整
  • R-BERTによるラベル再判定

Base Lineモデルの改良

今回のコンペは1月半ばに当時4位だった方公開したコードがコンペ終了までBase Lineとなっていました。

学習済みモデルの重みも公開されており「Forkしてそのままsubmitすれば同じスコアになる」状態であったため、多くの方がこの方と同じスコアになりました。

このコードのスコア自体が既に高かったですがそのままでメダルが取れるほど甘くはないので、githubで公開されていた学習用のコード（下記リンク）の改造をしました。

github.com

Base LineのモデルはLongfomerの出力層を全結合層に入れている形だったので、過去のコンぺの解法を参考にしながらLongfomerの出力層と全結合層との間にCNNやLSTMを追加したモデルを作りました。

www.ai-shift.co.jp

たったこれだけのことですが他の2つのアプローチがあまり効かなかったのでスコアへの貢献度は高かったです（ほぼこれだけでメダルが取れたと言っても過言ではない）。

後処理の閾値微調整

こちらのdiscussionでBase Lineのコードの後処理の閾値に改良の余地があるらしいことを知りました。

www.kaggle.com

これを見て、自分のモデルのCVの出力結果のnumpy.arrayを保存して後処理の閾値を微妙に変えながらCVのF1 scoreが良くなる閾値を探しました。

ただこれは自分で作ったコードで探索した閾値だとPublic scoreがあまり良くならなかったので、結局以下のコードで紹介されている閾値を使用しました。

[0.690]😄！try better parameters! | Kaggle

R-BERTによるラベル再判定

これはやってみましたがscoreが全く良くならなかったので、不採用とした案です。

きっかけとしては、単語単位での混合行列（下表）を見て「CounterclaimやRebuttalと予測すべきものを相当数Evidenceと誤判定している」という点に気づいたことがきっかけでした。

f:id:sue124:20220318142648p:plain

そこで「Counterclaim、RebuttalとEvidenceは同じような書き方をしているので、その文章の筆者がどういう立場かを考慮しないと判別が難しい」という仮説を立ててみました。 「Evidenceと判定した文章が筆者のPositionと合致するするかどうか」を以下の論文のR-BERTというモデルを使ってみることにしました。

arxiv.org

モデルのアーキテクチャーは下図の通りで、[CLS]と2つのspecial token ($, #) で囲まれた範囲のBERTの出力をAverage Poolingと全結合層で繋いで、2つのspecial tokenで囲まれた単語の関係性を予測するというものです。このモデルで SemEval2010 task 8 relational datasetのタスクでSoTAを達成したとのことです。

f:id:sue124:20220322070647p:plain
R-BERT モデルアーキテクチャー

このR-BERTを参考にして、1つ目のspecial tokenを文章中の「Position」につけて2つ目のspecial tokenを「Evidence」と判定した文章のうちの1文につけて「2つの文章が同じ立場かどうか」を判定するモデルを作成しました。

ただこの節の冒頭に記載した通り、このモデルはうまく機能しませんでした。

「Evidence」と「CounterclaimやRebuttal」の割合が1:1の時はまだいいのですが、実際の問題は上記の混合行列のようにこの割合がだいたい50:1ぐらいです。 このような偏ったデータで分類すると、偽陽性が大量発生してスコアが落ちてしまいました。

もう少し時間があればこのモデルを改良して「Positionを考慮して各単語を再分類する」ようなモデルもできたかもしれませんが、そこまでたどり着くことはできませんでした。

まとめ

今回はKaggle Feedback Prizeでやったことをまとめてみました。

銅メダルは取れましたが今回のコンペはBase Lineのレベルが高くて、自分のアプローチではあまりスコアが伸びなかったのが悔やまれるところです。 上位の方が公開してくれている解法を見て、さらにレベルアップしていきたいと思います。

お読みいただきありがとうございました。

G検定が機械学習初学者にも実務経験者にもおすすめできる良い資格だった件

G検定 データサイエンティスト データ分析

f:id:sue124:20210718140613p:plain

こんにちは、sue124です。

最近までG検定を受験するためにその出題範囲の勉強をしたところ、

「これは初心者にも、すでにある程度実務経験がある人にもおすすめできる」

と感じたので、今回はそのことに関して書いていきたいと思います。

G検定とは

G検定（ジェネラリスト検定）とは、一般社団法人日本ディープラーニング協会が実施している、ディープラーニングを事業に活かすための知識を有しているかを確認するための試験です。

日本ディープラーニング協会のサイトでは

「ディープラーニングの基礎知識を有し、適切な活用方針を決定して、事業活用する能力や知識を有しているかを検定する」

とされています。

www.jdla.org

G検定の試験では人工知能やディープラーニングに関する幅広い内容が出題されます。

以下では「初学者」と「実務経験者」に分けて、私がG検定をおすすめする理由を書いていきます。

おすすめする理由

機械学習初学者におすすめする理由

日本ディープラーニング協会は以下のサイトでG検定を以下のように定めています。

G検定は、すべてのビジネスパーソンが持つべきリテラシー

www.jdla.org

このような理念のもとで出題範囲が設定されているため、G検定の勉強をすることでビジネスにAI・ディープラーニングを適用するために必要な知識を一通り得ることができます。

その出題範囲は広く、1950年代の第一次AIブームに始まり、最新の技術トレンドや各国の政策が出題されます。

これを勉強すれば文字通り「すべてのビジネスパーソンが持つべきリテラシー」を身に付けられるので、「初学者が初手でG検定の勉強をする」というのは、非常に良い選択肢だと思います。

実務経験者におすすめする理由

G検定は実務経験者にもおすすめできます。

というのも、G検定の出題範囲は頻繁に見直されており、最新技術に関する問題もどんどん出題されます。
技術の移り変わりが早いこの業界において、これはかなりありがたいです。

最新の出題範囲（シラバス）は以下のサイトから取得できます。

www.jdla.org

2021年7月の最新版では、プルーニング、量子化のようなモデル軽量化や、OpenAI昨年発表されたGPT-3も入っており、最新の技術動向を追った上で深く勉強していないと答えられないものも含まれます。

G検定の出題範囲（シラバス）を追うことで、ある程度最新の技術動向をフォローすることができる、というのが実務経験者にもおすすめできる理由です。

すでにG検定を持っている人でも、上述のサイトの出題範囲（シラバス）を見てわからない単語があれば調べる、という使い方もおすすめです。

まとめ

今回は私が感じた「G検定の初学者にも実務経験者にもおすすめする理由」をまとめてきました。
これからも機械学習、AIに関する学習を続けていくので、定期的に他の人にもおすすめできる情報があれば定期的に発信していきたいと思います。

ここまでお読みいただき、ありがとうございました。